Bloom Filter详解

在我们设计一个算法的时候，经常要考虑时间效率和空间效率之间的平衡。以时间换空间，或者以空间换时间在大多数情况下都是不可避免的操作。如果我告诉你，有那么个数据结构，它在时间效率和空间效率上都很优秀，意外不意外，惊喜不惊喜？！

今天我们来讨论一个常用在大数据处理中的数据结构: 布隆过滤器 (Bloom Filter)。布隆过滤器的主要用途是用来检索一个元素是不是在一个集合中。 这是一个让人又爱又恨的数据结构。因为它占用很少的空间, 并提供常数时间的查询; 但同时, 它也有一些不可避免的缺点, 比如它有一定的误判率$($false positive rate$)$; 同时, 原始版本的Bloom Filter无法对元素进行删除操作。

这篇文章主要讨论以下内容:

• Bloom Filter的基本概念
• Bloom Filter主要参数的计算
• Bloom Filter的Java实现

Bloom Filter 简介

在数据处理的过程中, 我们最常遇到的操作之一就是membership查询。 所谓的membership查询就是想判断一个元素是否存在于一个给定的集合里。 最简单的做法是将集合数据存储在一个链表结构里, 然后每次查询的过程即为对链表的遍历过程。 当数据量变大时, 这种链表结构肯定是不够优化的, 因为每 次查询的时间复杂度为$O(n)$。 面试的时候经常有follow up问题, 让提高查询效率, 这个时候往往树状结构就要登场了, 因为它们可以使查询的效率变 为$O(logn)$。 当然树状结构还是可以被优化的, 就是用我们伟大的哈希方法, 比如Chain Hashing 和Bit Strings等, 或者就是简单的哈希表, 从而 得到 $O(\frac{n}{k})$的时间复杂度。 这里提句题外话, 面试的时候是可以根据题目的复杂度要求大概猜出需要用到的方法的, 虽然可能不是100%正确 , 但几乎可以猜个八九不离十。

这个时候, 如果面试官继续追问, 有没有时间和空间复杂度都更优的方法呢? 那么, 你就可以放心大胆的跟他说: yes, 有的, 它就是传说中的Bloom Filter。 Bloom Filter的思想非常简单。 一个Bloom Filter的物理结构其实是一个bit vector。 这个bit vector的每一位初始的时候都被设为0。 同时, 每个Bloom Filter 都伴随着k个hash functions。 往Bloom Filter插入元素的过程就是用每个hash function计算这个元素, 从而将结果所对应的比特位改为1。 如果当前比特位已经为1, 则在插入的过程保持这一位不变。

请看Bloom Filter示例图: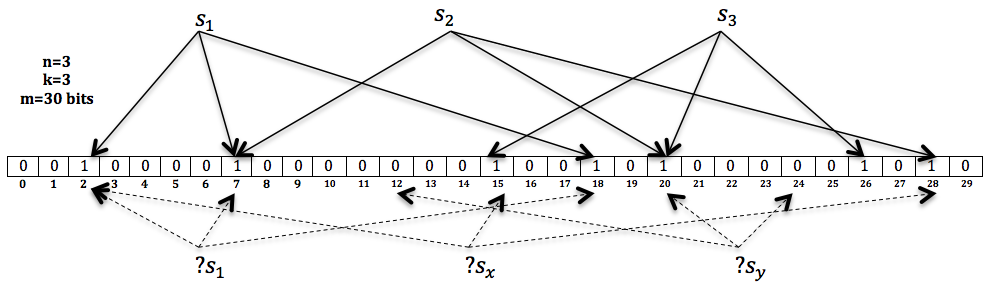

在这个示例中, 我们的Bloom Filter由一个30 bits的Bit Vector以及3个Hash Functions来构成。 我们将三个元素$S_1$, $S_2$和$S_3$分别插入这个Bloom Filter中。 然后对另外三个新元素$S_1$, $S_x$和$S_y$进行查询。 由图所示, $S_1$和$S_x$将被认为属于这个Bloom Filter, 因为所以相应的bit位均为1, 而$S_y$则被视为 不属于这个Bloom Filter。 但是, 其中$S_x$为一个false positive的答案, 因为在插入的时候我们并没有插入这个元素。False Positive的答案是由Hash Collision造成的。我们可以根据要插入的元素的个数来变化BF的长度，从而减少误判率。

Bloom Filter 主要参数的计算

影响Bloom Filter的性能的参数主要有四个:

• n : 需要插入Bloom Filter的最多的元素的个数
• m : Bloom Filter中bit位的个数
• k : Hash Functions的个数
• p : Bloom Filter的False Positive rate

其中需要插入Bloom Filter的最多元素的个数n我们是知道的, 或者至少是大致可以估算的。 所以构建一个Bloom Filter的时候, 主要需要设定bit位的个数, 从而来限制false positive rate 的大小。 或者控制false positive rate的大小在一个固定值, 从而推算Bloom Filter的bit位的长度。

在介绍Bloom Filter的参数计算之前, 我想先介绍一个概率理论中的经典呢模型, Balls into Bins模型。 这个模型在Computer Science领域有非常广泛的应用。 它涉及n个球和m个盒子。 每次, 随机将一个球投入其中一个盒子中。 将所有球都放在盒子中后, 我们观察每个盒子中球的数目。 我们将这个数目称为每个盒子的负载, 并且, 我们希望知道: 每个盒子的最大负载是多少。 Bloom Filter的思想很大程度借鉴了Balls and Bins问题。 不同的是, 我们用多个hash functions将每个”球”扔了多次。 而false positive则是与每个”盒子”的负载相关。 下面我们将一步步介绍 Bloom Filter中每个参数的计算方式。

我们首先来看一个引理:

Lemma 1: 用k个Hash Functions, 将n个元素插入到一个m bits的Bloom Filter中, 则这个Bloom Filter的任意一个bit位为0的概率将不会大于 $e^ {\frac{-k*n}{m}}$

这个Lemma计算Bloom Filter中任意一个bit位为0的概率, 计算的思路与计算balls into bins模型中任意一个盒子为空的概率类似。

证明： 用一个Hash Function插入一个元素后，某个特定bit位为0的概率为：$1 - \frac{1}{m}$

所以，用k个Hash Functions插入一个元素后，某个特定bit位为0的概率为：$(1 - \frac{1}{m})^{kn}$

并且：$\lim\limits_{m\to\infty}(1-\frac{1}{m})^{kn}=e^{\frac{-kn}{m}}$

Lemma 2: 假设我们运用Simple Uniform Hashing Functions对Bloom Filter进行插入操作，则这个Bloom Filter的False Positive率p是m，n和k的函数，并且p = $(1-e^{-\frac{nk}{m}})^k$

证明： Simple Uniform Hashing函数会将每一个元素以相等的概率hash去m个bit位中的一个。当用一个确定的hash函数处理一个确定的元素，某个特定的bit位$b_x$没有被设置为1的概率为：$1-\frac{1}{m}$

所以，当用k个Hash Function来处理这个元素的时候，某个特定的bit位$b_x$没有被设置为1的概率为：$(1-\frac{1}{m})^k$

然后，当用k个Hash Function来处理n个元素的时候，某个特定的bit位$b_x$没有被设置为1的概率为：$(1-\frac{1}{m})^{kn}$

相反，这个bit位被设置为1的概率为：$1-(1-\frac{1}{m})^{kn}$

在查询阶段，如果这个元素在Bloom Filter中对应的的所有hash bits都被设置为了1，则这个元素被认为存在于查询集中。所以False Positive的概率为：

p = $(1-(1-\frac{1}{m})^{kn})^k$

鉴于：

$\lim\limits_{x\to0}(1+x)^{\frac{1}{x}}=e$

$\lim\limits_{m\to\infty}(-\frac{1}{m})=0$

$\Rightarrow$ $\lim\limits_{m\to\infty}(1-(1-\frac{1}{m})^{kn})^k$ = $\lim\limits_{m\to\infty}(1-(1-\frac{1}{m})^{-m\times\frac{-kn}{m}})^k$ = $(1-e^{-\frac{nk}{m}})^k$

Lemma 3: 假设我们用k个hash functions将n个元素插入到一个含有m个bit位的Bloom Filter中，则非0bit位的个数的期望值是：$m\cdot(1-e^{\frac{-kn}{m}})$

证明： 假设$X_j$是一组随机变量的集合，并且当第j个bit位为0的时候$X_j$=1，反之$X_j$为0。则，根据Lemma 2， $E\left[X_j\right]$ = $(1-\frac{1}{m})^{kn} \approx e^{\frac{-kn}{m}}$

假设X为一个代表仍然为0的bit位的个数的随机变量，则：$E\left[X\right]$ = $E\left[\sum_{i=1}^{m} X_i\right]$ = $\sum_{i=1}^{m} E\left[X_i\right] \approx me^{\frac{-kn}{m}} $

所以非0bit位的个数的期望为：$m\cdot(1-e^{\frac{-kn}{m}})$

增加一个Bloom Filter的bit位的个数，可以减少发生Hash Collisions的几率，从而减少False Positive的概率。但是Bloom Filter的位数越多，它所占的硬盘空间就越大。在这里，我们假设，如果一个Bloom Filter一半的bit位被重置为1，则这个Bloom Filter达到了空间和Hash Collisions的平衡（当然这里你可以做其他假设）。 在这个假设前提下，我们可以来计算Bloom Filter主要参数之间的关系。

假设当一个Bloom Filter达到平衡状态的时候它含有n个元素，则下面这个方程描述了这个Bloom Filter的bit位的个数，与使用的hash function的个数及插入的元素个数之间的关系：$m = \frac{k \cdot n}{50\%} = 2 \cdot k \cdot n $ bits

Lemma 4: 当$e^{-\frac{nk}{m}}$ = $\frac{1}{2}$时， False Positive概率p达到最小值。此时：k = ln2 $\times \frac{m}{n}$， p = $\frac{1}{2}^k$ = $2^{-ln2 \times \frac{m}{n}}$

证明： 根据Lemma 2， $p$ = $(1-e^{-\frac{nk}{m}})^k$

所以，p可以被认为是k的一个函数：$p$ = $f(k)$ = $(1-e^{-\frac{nk}{m}})^k$

则：$f(k) = (1 - b^{-k})^k，b = e^{-\frac{n}{m}}$ （1）

对方程（1）两边取log值，可以得到：$ln[ f(k)] = k \cdot ln(1-b^{-k})$ （2）

对方程（2）两边求导，可以得到：$\frac{1}{f(x)} \cdot f’(x) = ln(1-b^{-k}) + k \cdot \frac{1}{1-b^{-k}} \cdot (-1) \cdot (-b^{-k}) \cdot ln(b) = ln(1-b^{-k}) + k \cdot \frac{b^{-k} \cdot ln(b)}{1-b^{-k}}$ （3）

当方程（3）等于0的时候，方程（2）达到最小值。这时可以得到：$ln(1-b^{-k}) + k \cdot \frac{b^{-k} \cdot ln(b)}{1 - b^{-k}} = 0$ （4）

$\Rightarrow (1- b^{-k}) \cdot ln(1- b^{-k}) = b^{-k} \cdot ln(b^{-k})$ （5）

根据方程（5）两边的对称性，可以得到：$1 - b^{-k} = b^{-k}$ （6）

$\Rightarrow e^{-\frac{kn}{m}} = \frac{1}{2}$ （7）

$\Rightarrow k = ln2 \cdot \frac{m}{n}$ （8）

所以：$p = f(k) = (1-\frac{1}{2})^{k} = (\frac{1}{2})^k = 2 ^ {ln2 \cdot \frac{m}{n}}$

由Lemma 4可以退出以下定理：

定理1： 已知一个Bloom Filter的False Positive为p，以及最多需插入元素的个数为n，则这个Bloom Filter的长度应为：$m = - \frac{n \cdot lnp}{(ln2)^2}$

需用到的Hash Function的个数应为：$k = ln2 \cdot \frac{m}{n} = log_2\frac{1}{p}$

删除Bloom Filter中的元素

在介绍Bloom Filter的实现之前，我希望先和大家探讨一下关于Bloom Filter中元素的删除的问题。上文介绍的传统的Bloom Filter是没有办法进行删除操作的，因为由于Hash Collision，如果单纯的把要删除的元素的相应bit位重置为0会误删掉其他元素。

为了解决这一问题，我们可以把每个bit位换成一个counter，要删除某个元素的时候可以减少相应位的counter，这种Bloom Filter的变种被称为Counting Bloom Filter。它虽然为Bloom Filter增加了删除操作，但是它也同时增加了Bloom Filter的’占地面积’。

那么有没有可能仍然用bit vector作为Bloom Filter的实现，同时增加删除功能呢？答案是有的，我最欣赏的一种实现叫Shifting Bloom Filter。它是由2016年一篇VLDB上的文章提出的，在这里我们简单介绍一下它的思想。在这篇文章中，作者发现通常我们需要再Bloom Filter中 存储两类信息，（1）元素是否存在于数据集中（2）元素的附加信息。传统BF已经能很好的解决（1），在SFB中作者用一个offset来存储元素的附加信息，这个offset也是一个hash function，在将$h_i(e)$设置为1的同时，SFB将$h_i(e)+o(e)$也设置为1。感兴趣的同学可以阅读这篇文章。 我们不再赘述。

如果你也有自己偏爱的BF的变种，欢迎写邮件与我讨论。写邮件请按左侧信息栏，我的头像下方的信封按钮=^-^=。

Bloom Filter的Java实现

我总觉得实现部分最简单直接粗暴的方法就是放代码:P 。 代码中有详细的注解，这里我们就不再重复。

如果您觉得本文有用, 请扫描一下二维码, 随意打赏 =^-^=