2016 December 16

LeetCode刷题记之Range Sum Query

今天想要讨论的问题是Range Sum Query。LeetCode有三个相关问题: Range Sum Query - Immutable、 Range Sum Query - Mutable 和 Range Sum Query 2D - Mutable (最后那道题是付费题)。

我们今天主要讨论前面两道题。

Range Sum Query - Immutable

这道题的题目很简单, 就是给定一个数组, 想要求这个数组, 从第i位到第j位的和。我们当然可以用O$($n$)$的复杂度从第i位遍历到第j位, 一路加过去。不过再仔细想想, 问题应该没有那么简单吧, 这种做法考初学者的考试都不屑于考。而且, 题目中有补充说明, 这个叫getRangeSum$($int i, int j$)$的method会经常被call, 再看看题目的归类, 它被归到了动态规划类中。动态规划的思想是把子问题的结果存在一个数组中, 然后每次调用这个数组的相应位。这会儿你可能就恍然大悟了吧, 嘿嘿哈嘿, 将数组的第i位存储为a[0]加到a[i] 的和即可, 然后getRangeSum其实就是做减法嘛, sum[j] - sum[i-1]。这是一道非常简单的动态规划。

代码就不贴在这里了, 请参考这里。

Range Sum Query - Mutable

现在, 我们把上面这道题稍微变换一下。这一次, 增加一个叫做update$($int i, int val$)$的方法, 将数组的第i位换成val。其他条件不变, 仍然是会多次call getSum 和 update。这回上一道题的解法就不太划算了。因为, update的时候, 会将第i位之后的所有位都改变。那有没有什么方法可以仍然用我们做上一题的思想, 但是update的时候不要改动”那么多”的元素呢? 答案当然是有的, 这个方法叫做Binary Index Tree。

这个Tree的逻辑是一个树, 但其实它的存储结构是一个数组。它的提出一开始是用于计算数据的压缩中的累积频率 — 这是什么鬼, 其实我也不知道; 现在它常被用在高效的计算数列的前缀和、区间和。它的思路来源于: 所有整数都可以表示成2的幂和, 那么一串数列当然也可以表示成一系列子序列的和。根据这一思想, 我们可以将一个前缀和划分成多个子序列的和, 而划分的方法与数的2的幂和表示极其相似。并且, 子序列的个数是这个数二进制表示中1的个数。—多么神奇!

Let’s have a look at an example:

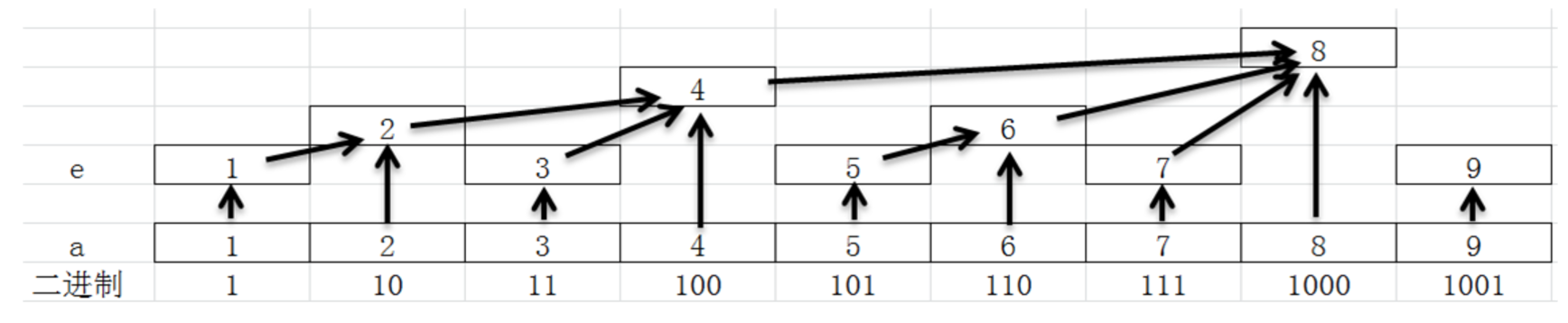
在这个图中a[]为原始数据, e[]为树状数组。

在图中我们可以发现一个有趣的规律, — 其实我没发现 -_-b。就是如果一个数m的二进制的表达中末尾有n个连续的0, 则e[m]为a中从a[m]起往前算2^n个连续的数相加, 而末尾的0的个数没有那么好求, 但是这个问题可以转化为第一个1所在的位数, 问题将会变得好求很多。

比如:

4 = 100 –> 2^2 ===> e[4] = a[4] + a[3] + a[2] + a[1]
6 = 110 –> 2^1 ===> e[6] = a[5] + a[6]
7 = 111 –> 1^0 ===> e[7] = a[7]

为了更好的理解这个算法, 我们来介绍两个概念:

后继节点: $($可理解为父节点$)$ 一个节点的后继节点是离它最近的, 比它大的, 末尾的0比它多的那个节点。以图中的节点为例, 2的后继节点是4, 5的后继节点是6。 — 用来计算e数组, 将当前计算出来的e[i]添加到他们的后继中
前驱节点: $($可理解为子节点$)$ 一个节点的前驱节点是离它最近的, 比它小的, 末尾的0比它多的那个节点。以图中的节点为例, 7的前驱节点是6, 6的前驱节点是4。 — 避免计算连续和的时候进行重复计算

为了计算前驱节点和后继节点, 我们需要首先找到一个数X的二进制表示中, 最后一位1在什么位置。所谓的最后一位1, 是从2^0位开始往前数, 第一个遇到的1, 也就是2^1上的1。这个1的位置的求法是: ((NOT X)+1) AND X。

For example:

34的二进制表示为: 100010。最后一位1为表黑体的部分: 100010。NOT 34的结果是011101, 加1后为: 011110, 011110 AND 100010的结果是: 000010, 即为2。

让我们写一个方法叫做lowestBit, 用来返回最后一位1的位置:

private int lowestBit(int i){
    return x & -x;
}

有了这个最后一位1之后, 前驱节点和后继节点就好办了。因为: e[X] 的前驱节点为: e[X - lowestBit$($X$)$] e[X] 的后继节点为: e[X + lowestBit$($X$)$]

而e数组与a数组的关系为:

e[i] = $\sum_{j = i - lowestBit(i) + 1}^{i} a[j]$

写到这里, 让我们写另外一个method来计算初始的e数组。

private int[] createBIT(int[] nums){
    int[] BIT = new int[nums.length];
    
    for(int i=1; i<=nums.length; i++){
        BIT[i] = nums[i];
        
        for(int j= i - lowestBit(i) +1 ; j <i; j++){
            BIT[i] = BIT[i] + nums[j];
        }
    }
}

如果对a数组的第j位进行了update, 那就意味着e数组中利用了这一位的所有位都需要相应进行update。而利用了它的节点为它的后继节点, 而每个节点的后继节点为j = j + lowestBit(j), 如此向后递归:

public void update(int i, int val){
    for(int j=i; j<= nums.length; j = j + lowestBit(j)){
        BIT[j] = BIT[j] + val;
    }
}

而求和的运算也变得相应的容易了, 因为sum[X] 为X的前驱节点的和, 如此向前递归

public int getSum(int i){
    int sum = 0;
    for(int j = i; j > 0; j = j - lowestBit(j)){
       sum += BIT(j); 
    }
    return sum;
}

这样就可以像第一道题那样来计算range sum了:

public int getRangeSum(int i, int j){
    return getSum(j) - getSum(i);
}

完整代码请参考这里。

如果您觉得本文有用, 请扫描一下二维码, 随意打赏 =^-^=